ELEMENTI DI ARCHEOASTRONOMIA

Un altro corpo celeste che anticamente assunse per queste popolazioni un'importanza fondamentale è la Luna. Vediamo di capire meglio il suo comportamento in cielo che è molto più complicato di quello del Sole. Al fine di comprendere meglio la problematica connessa con l'osservazione della Luna da parte degli antichi è necessario descrivere, almeno sommariamente, le caratteristiche principali del complicato moto apparente del nostro satellite naturale, nel cielo. La Luna rivoluisce intorno alla Terra muovendosi su una orbita ellittica, la cui orientazione è variabile lentamente nel tempo, ad una distanza media di circa 60 volte il raggio del nostro pianeta. La distanza tra la Terra e la Luna aumenta di circa 4,4 cm ogni anno a causa del trasferimento di momento angolare dalla Terra alla Luna come conseguenza dell'attrito mareale tra questi due corpi celesti. Ad esempio, mediamente, durante l'età del Ferro, il periodo aureo della cultura celtica, la Luna era più vicina alla Terra di circa 110 metri. A causa delle leggi della meccanica orbitale il trasferimento di momento angolare dalla Terra alla Luna causa anche il rallentamento del moto di rotazione del nostro pianeta e quindi la durata del giorno siderale si allunga leggermente durante i secoli e i millenni. Quando si ricostruiscono le condizioni di visibilità delle eclissi avvenute nell'antichità è sempre necessario tenere conto di questa variazione. Le distanze estreme raggiunte dalla Luna durante la sua orbita sono rispettivamente 55,4 volte il raggio medio terrestre, la minima al perigeo e 66.1 volte la massima, all'apogeo.

I nodi dell’orbita della Luna

La linea ideale congiungente l'Apogeo e il Perigeo è detta linea degli Apsidi la quale ruota, in senso diretto, cioè in direzione del moto orbitale della Luna, a causa delle perturbazioni gravitazionali combinate dovute alla Terra e al Sole, in modo tale che in 3232,59 giorni solari medi venga compiuto un giro completo rispetto alla posizione delle stelle sulla sfera celeste. I punti di intersezione tra l'orbita lunare e il piano dell'orbita terrestre sono detti Nodi. Il nodo ascendente corrisponde al punto in cui la Luna attraverso il piano orbitale delle Terra salendo da latitudini eclittiche negative (australi) a latitudini positive (boreali). Il nodo discendente, invece corrisponde al punto di intersezione in cui la Luna scende dalle latitudini eclittiche boreali a quelle australi. Questi due particolari punti si muovono sotto l'effetto combinato dell'attrazione gravitazionale del Sole e della Terra sulla Luna. Il moto dei nodi dell'orbita lunare è retrogrado cioè diretto in senso opposto rispetto alla direzione del moto della Luna nella sua orbita. Una rotazione completa dei nodi richiede 6793,39 giorni solari che corrispondono a 18,61 anni solari; questo valore numerico è molto importante dal punto di vista storico ed archeoastronomico. Durante una completa rivoluzione sinodica media pari a 29,5306 giorni, cioè un ciclo completo di fasi lunari, la Luna descrive sulla sfera celeste, poco più di un cerchio completo inclinato di 5°,15 rispetto al cerchio dell'Eclittica, valore anche questo soggetto a variazione nel tempo. La variazione in questo caso è di tipo periodico ed ha una ampiezza di 0°,15 gradi e un periodo di 173,3 giorni. Anche questo valore rappresenta un numero importante dal punto di vista storico, infatti esso è la metà del cosiddetto "Anno delle Eclissi" che quindi comprende 346,6 giorni solari medi. Il particolare valore dell'inclinazione dell'orbita della Luna, implica che nelle regioni geografiche corrispondenti all'Europa, durante l'inverno, nelle notti di plenilunio, la Luna sia visibile molto alta nel cielo. Durante l'estate invece si verifica la situazione opposta, cioè nelle notti di plenilunio la Luna è posizionata bassa sull'orizzonte.

Le periodicità della Luna

La Luna presenta molte periodicità tra le quali annoveriamo il mese sinodico e il mese siderale che sono di grande importanza dal punto di vista archeoastronomico. Il mese sinodico è definito come l'intervallo richiesto alla Luna per passare da una determinata fase alla successiva dello stesso tipo, per esempio da un plenilunio al successivo. La lunghezza del mese sinodico lunare vale 29,5306 giorni solari medi. Il mese siderale lunare invece è l'intervallo che intercorre tra due passaggi consecutivi della Luna presso la medesima configurazione di stelle. La lunghezza del mese siderale vale 27,322 giorni solari medi, quindi risulta essere più corto di circa 2 giorni rispetto a quello sinodico. Ragionando dal punto di vista dello sviluppo dei calendari lunisolari è necessario prendere in esame anche altre due periodicità: le rivoluzioni Draconitica e Anomalistica. Il fenomeno della retrogradazione dei nodi lunari, la cui periodicità è 18,61 anni solari tropici, venne probabilmente scoperto solamente in maniera indiretta sulla base dell'osservazione della cadenza delle eclissi, oppure in seguito ad un lungo e continuo lavoro di osservazione dello spostamento dei punti di sorgere e di tramontare dell'astro all'orizzonte naturale locale. Il nodo ascendente dell'orbita lunare, per effetto del suo moto retrogrado si muove in modo da andare incontro alla Luna, quindi l'intervallo tra due passaggi consecutivi allo stesso nodo è più corto se paragonato al periodo di rivoluzione siderale. Questo periodo e detto Periodo Draconitico e vale attualmente 27 giorni, 5 ore, 5 minuti e 35.8 secondi di tempo medio. Il periodo di rivoluzione Anomalistica è l'intervallo tra due passaggi della Luna al perigeo, cioè l'intervallo di tempo richiesto per tornare due volte consecutive nello stesso punto della sua orbita. La durata della rivoluzione Anomalistica è 27 giorni, 13 ore, 18 minuti e 33.1 secondi di tempo medio. Infine abbiamo la rivoluzione Tropica che rappresenta l'intervallo di tempo tra due congiunzioni eclittiche successive tra la Luna e il punto Gamma o punto equinoziale primaverile, cioè il punto occupato annualmente dal Sole nell'istante in cui avviene l'equinozio di primavera. La rivoluzione tropica è più corta della rivoluzione siderea di circa 7 secondi perché la direzione del punto equinoziale primaverile non è fissa nello spazio, ma per effetto del fenomeno della Precessione si sposta in senso retrogrado lungo l'Eclittica andando incontro alla Luna. Riassumendo, esistono quindi cinque tipi di rivoluzioni lunari: 1) la rivoluzione Sinodica (detta anche lunazione), 2) la rivoluzione Tropica, 3) la rivoluzione Siderale, 4) la rivoluzione Draconitica, 5) la rivoluzione Anomalistica; appare quindi evidente che il moto apparente del nostro satellite naturale è così complesso che un gran numero di famosi matematici tra i quali Newton, Gauss, Eulero, Laplace, Delaunay e molti altri dedicarono gran parte della loro vita a sviluppare metodi di calcolo che fossero in grado di prevedere con la massima accuratezza possibile la posizione apparente della Luna nel cielo. Tutti questi sforzi vennero compiuti negli anni che vanno da XVII secolo in poi sotto la spinta della necessità di determinare con la massima accuratezza possibile la posizione delle navi in mare durante la navigazione oceanica. I matematici dei secoli scorsi affrontarono il problema armati delle più efficienti tecniche di calcolo disponibili a quei tempi; invece con molta probabilità sia chi osservava il cielo durante la preistoria che i più recenti druidi celtici tentarono, senza alcun formalismo matematico, ma utilizzando il ragionamento, di raggiungere il maggior accordo possibile tra le posizioni previste e la effettiva ubicazione apparente della Luna sulla sfera celeste riuscendoci piuttosto bene, soprattutto questi ultimi. Questo lavoro venne svolto soprattutto per necessità di sviluppare dei calendari efficienti.

Il movimento dei punti di levata e tramonto della Luna

Come abbiamo visto l'orbita della Luna interseca quella della Terra in due punti: i nodi che sono soggetti al fenomeno periodico della retrogradazione; inoltre l'orbita del nostro satellite naturale è inclinata rispetto a quella della Terra di un angolo, chiamato “i” e pari, in media, a 5°,15. L'Eclittica invece è inclinata rispetto all'equatore celeste di un angolo, detto "e", pari attualmente a 23°,45 e lentamente variabile nel tempo oscillando grosso modo da 22° a 24° in un periodo di 41013 anni. Durante la retrogradazione può accadere che, ad una certa epoca, il nodo ascendente vada a coincidere con la posizione del punto Gamma, cioè il punto di intersezione tra l'equatore celeste e l'eclittica, corrispondente alla posizione del Sole nell'istante dell'equinozio di primavera. In questo caso avviene che la Luna, muovendosi lungo la sua orbita, può raggiungere il punto di massima distanza angolare al di sopra dell'equatore celeste, cioè la sua massima declinazione boreale geocentrica, la quale sarà pari a d=(+e+i) vale a dire 28°,6. Questo fenomeno è avvenuto l'ultima volta il 15 settembre 2006.

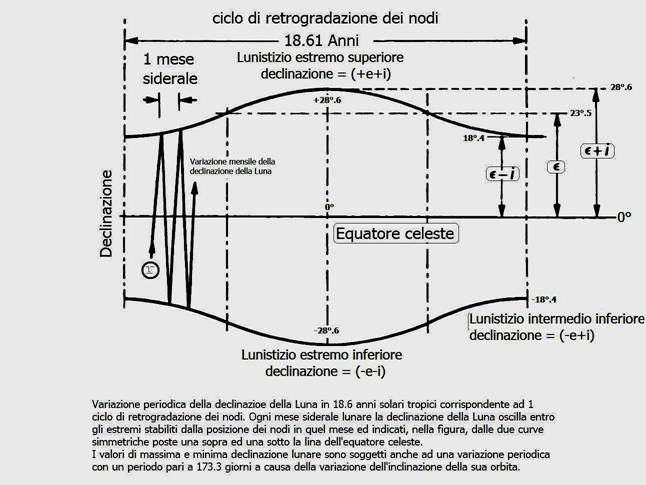
n quel giorno la Luna, in un dato luogo, sorgerà molto a nord, più a settentrione rispetto al punto di levata del Sole al solstizio d'estate, durante il quale l'astro diurno arriva ad avere una declinazione pari solamente a d=+e. La Luna allora si dice essere al "lunistizio estremo superiore" e il suo punto di levata all'orizzonte astronomico locale è detto punto d'arresto superiore. L'azimut, di levata della Luna, contato dalla direzione nord del meridiano astronomico locale muovendosi positivamente ad est, allora assumerà il minimo valore consentito durante il ciclo di 18,6 anni. Questo valore dipenderà anche dalla latitudine del luogo di osservazione e sarà numericamente tanto minore, maggiormente il luogo di osservazione si avvicina al polo nord della Terra. Una situazione interessante si verifica qualora il luogo di osservazione sia posto ad una latitudine maggiore o uguale a j=(90°-e-i), in questo caso l'astro notturno diventa temporaneamente circumpolare e anche questo fenomeno si ripete ogni 18,61 anni. Attualmente la latitudine critica perchè il fenomeno possa essere visibile vale 61°.4.

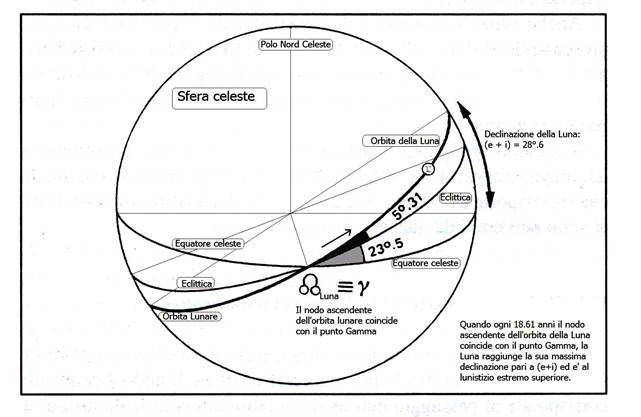
A questo proposito è interessante ricordare l'affermazione di Ecateo di Mileto che nel VI secolo a.C. riferiva di un tempio circolare, posto nel paese degli Iperborei (coloro che vivono "sotto l'Orsa Maggiore"), in cui la Luna ogni 19 anni "danzava lungo l'orizzonte" senza mai tramontare. Il tempio fu per molti anni erroneamente identificato con Stonehenge, cosa impossibile a causa del fatto che la latitudine del complesso megalitico britannico è troppo bassa affinché questo fenomeno potesse mai verificarsi. In seguito a studi recenti A. Gaspani ha proposto l'identificazione del tempio citato da Ecateo di Mileto, con il sito megalitico di Callanish, nell'Isola di Lewis, a nord della Gran Bretagna, luogo in cui il fenomeno poteva effettivamente essere osservato.

Nei luoghi posti a latitudini maggiori di j=(90°-e-i), mezzo mese draconitico dopo il lunistizio superiore, cioè 13,6 giorni, l'astro percorrerà la sua traiettoria nel cielo rimanendo sempre sotto l'orizzonte astronomico locale. In prossimità di quei giorni la traiettoria lunare andrà gradualmente abbassandosi fino ad essere percorsa interamente sotto il profilo dell'orizzonte. Quando la Luna si trova al lunistizio estremo superiore e quindi il suo punto di levata all'orizzonte astronomico locale è posizionato al punto d'arresto superiore, allora quella notte l'astro culminerà molto alto e passerà al meridiano alla sua massima altezza. Mezzo mese draconitico dopo, avendo la Luna percorso metà della sua orbita, essa si troverà nella posizione opposta per cui la sua declinazione raggiungerà il minimo valore possibile pari a d=(-e-i), raggiungendo il lunistizio estremo inferiore, quindi -28°,6 , ragionando con i valori attuali (anno 2007) di "e" ed "i".

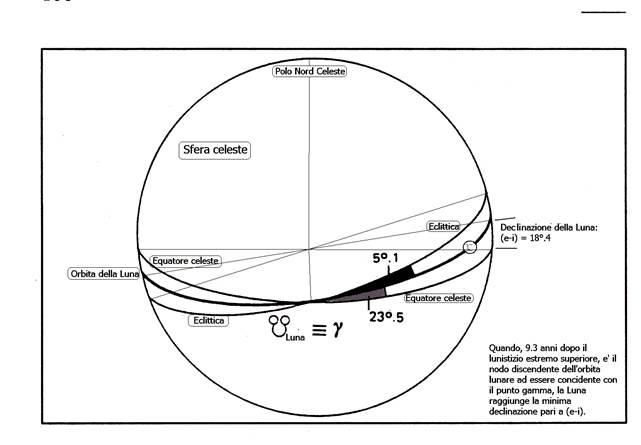
Appare allora evidente che il suo punto di levata sull'orizzonte astronomico sarà spostato più a sud del punto di levata del Sole al solstizio d'inverno. Tale punto sarà quindi indicato, anche lui, col nome di punto d'arresto superiore in quanto la declinazione della Luna è massimamente negativa ed il punto di levata è quello di massimo azimut consentito per una determinata latitudine geografica. In quella notte particolare la Luna sorgerà nella direzione sud-est, rimanendo però molto bassa sull'orizzonte durante il suo movimento nel cielo e tramonterà in direzione sud-ovest. I punti di tramonto degli astri sono simmetrici ai punti di levata rispetto alla linea del meridiano astronomico locale quindi quando la Luna sorge a nord-est tramonterà a nord-ovest e quando sorge a sud-est tramonterà a sud-ovest. Prima del 200 a.C. le declinazioni geocentriche estreme della Luna potevano raggiungere, a causa del fatto che il valore dell'obliquità dell'eclittica era un poco maggiore dei valori attuali, valori superiori ai 29° sopra e sotto l'equatore celeste, quindi anche i punti d'arresto superiore ed inferiore erano un pò più distanti l'uno dall'altro. A questo punto appare di notevole interesse prendere in esame contemporaneamente sia la posizione del Sole e quella della Luna e fare alcune considerazioni. In questo caso si rileva che se l'epoca in cui la Luna è al lunistizio superiore (massima declinazione) in coincidenza con il solstizio estivo, allora l'astro deve giungere in questo particolare punto della sua orbita alla fase di Luna nuova e quindi, mezzo mese dopo essa giunge invece alla sua minima declinazione poco prima del plenilunio. Nel caso il lunistizio superiore coincida con il solstizio invernale, allora la Luna raggiungerà la sua massima declinazione quando è piena e mezzo mese draconitico dopo, al lunistizio estremo inferiore, (minima declinazione) poco prima del novilunio.

Punti di levata e di tramonto della Luna ai lunistizi

Dopo 9,3 anni, poiché la linea dei nodi ha retrogradato di 180°, il nodo ascendente coinciderà con il punto di Libra, opposto a quello d'Ariete. In questo caso la Luna si troverà ai lunistizi intermedi, cioè la massima e la minima declinazione raggiungibili saranno rispettivamente d=(e-i) e, mezzo mese draconitico dopo, d=(-e+i), cioè rispettivamente 18°,3 sopra e 18°,3 gradi sotto l'equatore celeste. Quando la declinazione della Luna vale d=(e-i) l'astro sorgerà in corrispondenza di un punto dell'orizzonte astronomico locale posto più a sud rispetto al punto di levata del Sole al solstizio d'estate, ma più a nord rispetto al punto di levata dell'astro diurno agli equinozi. Mezzo mese draconitico dopo, la declinazione raggiunta dalla Luna sarà pari a d=(-e+i) e quindi il suo punto di levata, all'orizzonte astronomico locale, sarà intermedio tra le posizioni della levata solare equinoziale e quella solstiziale invernale. Queste due particolari posizioni vanno sotto il nome di punti d'arresto inferiori.

Variazione della declinazione della Luna ai lunistizi dall’anno -4000 al +2000.

Appare allora molto evidente che nel passaggio tra le declinazioni d=(e-i) e d=(-e+i), l'escursione dell'altezza della Luna nel cielo durante il mezzo mese draconitico è consistentemente minore di quella che si rileva quando l'astro è posto alle declinazioni massime.

Riassumendo quanto detto possiamo allora affermare che nel caso della Luna è necessario considerare i quattro punti fondamentali di levata nell'arco orientale dell'orizzonte astronomico locale e i corrispondenti quattro punti di tramonto nell'arco occidentale. Tenendo conto anche dei punti di levata e tramonto del Sole ai solstizi e agli equinozi, rileviamo che dal punto di vista archeoastronomico, escludendo le stelle, dobbiamo considerare ben 14 posizioni (8 lunari e 6 solari) di cui la metà al sorgere e l'altra metà al tramonto. Rimane ora da porsi una domanda fondamentale e cioè a cosa potesse servire ad una popolazione antica conoscere le epoche e la posizione dei lunistizi. Questa è una domanda a cui, nello stato attuale delle ricerche, è molto difficile rispondere in quanto il ciclo di retrogradazione dei nodi non ha rilevanza pratica, per esempio dal punto di vista agricolo anche se un'interessante ipotesi è stata recentemente avanzata da Adriano Gaspani. Potremmo forse ipotizzare che qualora la Luna fosse stata prossima al lunistizio corrispondente alla declinazione massima (d=e+i) essa avrebbe percorso un grande arco in cielo rimanendo quindi sopra l'orizzonte per quasi tutta la notte, soprattutto qualora l'astro fosse stato al plenilunio e la latitudine del luogo fosse stata relativamente alta. In questo caso la Luna poteva essere molto utile per il fatto che la sua luce poteva illuminare il cammino durante gli spostamenti notturni, mentre mezzo mese draconitico dopo, l'arco descritto sopra l'orizzonte durante la notte era piccolo, e l'illuminazione notturna durava poche ore.

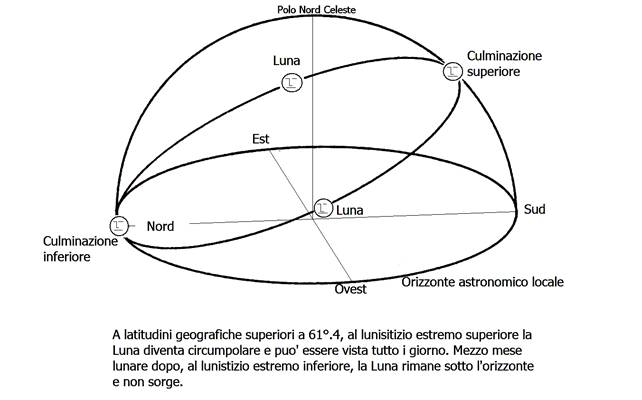
Questa ipotesi però risulta poco convincente in quanto le declinazioni massime si ripetono ogni 18,6 anni, periodo per la verità piuttosto lungo per programmare spostamenti da effettuarsi in un numero limitato di notti. L'esistenza dei numerosi allineamenti su questi particolari punti d'arresto sperimentalmente rilevati in una grande quantità di siti europei che si collocano cronologicamente dalla preistoria alla proto-storia è, però, un dato di fatto che non può essere trascurato; ecco che la valenza rituale della Luna potrebbe essere una giustificazione più appropriata per spiegare l'esistenza degli allineamenti rilevati.

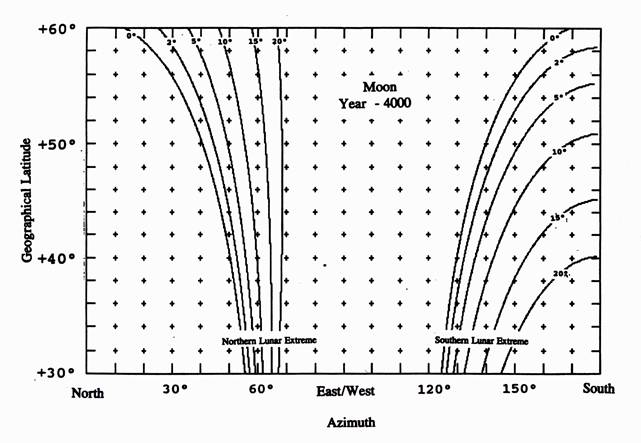
Variazione dei punti di levata della Luna al lunistizio estremo superioe e al lunistizio estremo inferire, nell’anno -4000, calcolata per un intervallo di latitudine geografica compreso tra 30° e 60° Nord. Le varie curve sono calcolate per un’altezza dell’orizzonte natuale locale compresa tra 0° e 20°.

La declinazione della Luna è condizionata da tre termini periodici fondamentali a cui se ne aggiungono altre migliaia di entità però molto più piccola e rilevanti qualora la posizione dell'astro sia richiesta con grande precisione nel cielo. Il primo termine è quello con periodicità pari ad un mese draconitico (27,21 giorni) che corrisponde al ritorno dell'astro allo stesso nodo della sua orbita, e ampiezza pari ad "e", legato alla rivoluzione della Luna intorno alla Terra. Il secondo termine è quello con periodicità pari a 18,61 anni solari tropici ed è il periodo di retrogradazione di nodi.

La sua ampiezza è pari a "i" cioè l'angolo con cui l'orbita lunare è inclinata rispetto a quella della Terra. Il terzo ciclo, dovuto alla perturbazione gravitazionale del Sole sulla Luna, corrisponde all'oscillazione periodica del valore dell'inclinazione dell'orbita lunare, con un ampiezza di 8,7 minuti d'arco e un periodo di 173.3 giorni, metà del cosiddetto anno delle eclissi, che corrisponde all'intervallo di tempo che separa due periodi dell'anno nei quali si possono verificare questi fenomeni. Questa periodicità fu scoperta da Tycho Brahe durante il XVI secolo. Tale piccolo spostamento, quando giunge al massimo, può indicare l'epoca di una possibile eclisse di Sole o di Luna. Un altro fatto importante è che la conoscenza del ciclo lunistiziale lunare poneva in mano, a chi lo conosceva, lo strumento per prevedere alcune eclissi, soprattutto quelle di Luna. Infatti qualora la Luna si trovi alla massima o minima declinazione possibile e contemporaneamente al primo o all'ultimo quarto allora sette giorni dopo è possibile il verificarsi di un eclisse di Sole o di Luna in quanto l'astro si troverà al nodo e contemporaneamente al novilunio o al plenilunio, quindi con il Sole anche lui posizionato ad un dei due nodi dell'orbita lunare. Questo metodo è in teoria possibile e praticabile, ma permette la predizione di un numero piuttosto limitato di eclissi e soprattutto a scadenza breve, solo 7 giorni. Lo studio del succedersi delle epoche di lunistizio avrebbe però forse potuto contribuire efficacemente, dopo un certo tempo, all'identificazione del numero di lunazioni corrispondenti a valori interi degli intervalli di 173,3 giorni, le quali costituirono soprattutto in epoca antica utili predittori per le sequenze di eclissi.

(Continua-)

Autore:Adriano Gaspani, aprile 2008)

Sezioni correlate in questo sito:

	1^ parte di questo lavoro
	Archeoastronomia

www.duepassinelmistero.com Avvertenze/Disclaimer

pubblicato in settembre '09